Understanding word vectors

... for, like, actual poets. By Allison Parrish

In this tutorial, I'm going to show you how word vectors work. This tutorial assumes a good amount of Python knowledge, but even if you're not a Python expert, you should be able to follow along and make small changes to the examples without too much trouble.

This is a "Jupyter Notebook," which consists of text and "cells" of code. After you've loaded the notebook, you can execute the code in a cell by highlighting it and hitting Ctrl+Enter. In general, you need to execute the cells from top to bottom, but you can usually run a cell more than once without messing anything up. Experiment!

If things start acting strange, you can interrupt the Python process by selecting "Kernel > Interrupt"—this tells Python to stop doing whatever it was doing. Select "Kernel > Restart" to clear all of your variables and start from scratch.

Why word vectors?

Poetry is, at its core, the art of identifying and manipulating linguistic similarity. I have discovered a truly marvelous proof of this, which this notebook is too narrow to contain. (By which I mean: I will elaborate on this some other time)

Animal similarity and simple linear algebra

We'll begin by considering a small subset of English: words for animals. Our task is to be able to write computer programs to find similarities among these words and the creatures they designate. To do this, we might start by making a spreadsheet of some animals and their characteristics. For example:

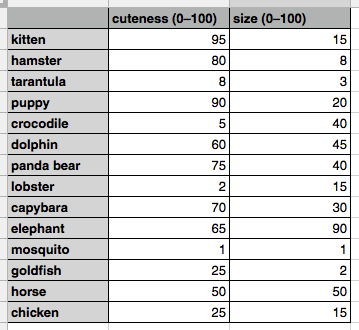
This spreadsheet associates a handful of animals with two numbers: their cuteness and their size, both in a range from zero to one hundred. (The values themselves are simply based on my own judgment. Your taste in cuteness and evaluation of size may differ significantly from mine. As with all data, these data are simply a mirror reflection of the person who collected them.)

These values give us everything we need to make determinations about which animals are similar (at least, similar in the properties that we've included in the data). Try to answer the following question: Which animal is most similar to a capybara? You could go through the values one by one and do the math to make that evaluation, but visualizing the data as points in 2-dimensional space makes finding the answer very intuitive:

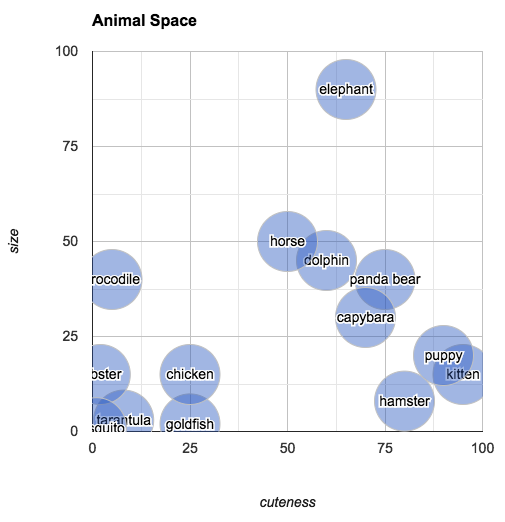
The plot shows us that the closest animal to the capybara is the panda bear (again, in terms of its subjective size and cuteness). One way of calculating how "far apart" two points are is to find their Euclidean distance. (This is simply the length of the line that connects the two points.) For points in two dimensions, Euclidean distance can be calculated with the following Python function:

(The ** operator raises the value on its left to the power on its right.)

So, the distance between "capybara" (70, 30) and "panda" (74, 40):

... is less than the distance between "tarantula" and "elephant":

Modeling animals in this way has a few other interesting properties. For example, you can pick an arbitrary point in "animal space" and then find the animal closest to that point. If you imagine an animal of size 25 and cuteness 30, you can easily look at the space to find the animal that most closely fits that description: the chicken.

Reasoning visually, you can also answer questions like: what's halfway between a chicken and an elephant? Simply draw a line from "elephant" to "chicken," mark off the midpoint and find the closest animal. (According to our chart, halfway between an elephant and a chicken is a horse.)

You can also ask: what's the difference between a hamster and a tarantula? According to our plot, it's about seventy five units of cute (and a few units of size).

The relationship of "difference" is an interesting one, because it allows us to reason about analogous relationships. In the chart below, I've drawn an arrow from "tarantula" to "hamster" (in blue):

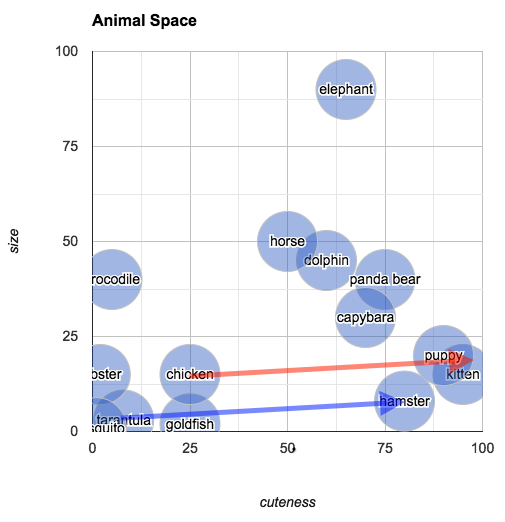
You can understand this arrow as being the relationship between a tarantula and a hamster, in terms of their size and cuteness (i.e., hamsters and tarantulas are about the same size, but hamsters are much cuter). In the same diagram, I've also transposed this same arrow (this time in red) so that its origin point is "chicken." The arrow ends closest to "kitten." What we've discovered is that the animal that is about the same size as a chicken but much cuter is... a kitten. To put it in terms of an analogy:

Tarantulas are to hamsters as chickens are to kittens.

A sequence of numbers used to identify a point is called a vector, and the kind of math we've been doing so far is called linear algebra. (Linear algebra is surprisingly useful across many domains: It's the same kind of math you might do to, e.g., simulate the velocity and acceleration of a sprite in a video game.)

A set of vectors that are all part of the same data set is often called a vector space. The vector space of animals in this section has two dimensions, by which I mean that each vector in the space has two numbers associated with it (i.e., two columns in the spreadsheet). The fact that this space has two dimensions just happens to make it easy to visualize the space by drawing a 2D plot. But most vector spaces you'll work with will have more than two dimensions—sometimes many hundreds. In those cases, it's more difficult to visualize the "space," but the math works pretty much the same.

Language with vectors: colors

So far, so good. We have a system in place—albeit highly subjective—for talking about animals and the words used to name them. I want to talk about another vector space that has to do with language: the vector space of colors.

Colors are often represented in computers as vectors with three dimensions: red, green, and blue. Just as with the animals in the previous section, we can use these vectors to answer questions like: which colors are similar? What's the most likely color name for an arbitrarily chosen set of values for red, green and blue? Given the names of two colors, what's the name of those colors' "average"?

We'll be working with this color data from the xkcd color survey. The data relates a color name to the RGB value associated with that color. Here's a page that shows what the colors look like. Download the color data and put it in the same directory as this notebook.

A few notes before we proceed:

• The linear algebra functions implemented below (addv, meanv, etc.) are slow, potentially inaccurate, and shouldn't be used for "real" code—I wrote them so beginner programmers can understand how these kinds of functions work behind the scenes. Use numpy for fast and accurate math in Python.
• If you're interested in perceptually accurate color math in Python, consider using the colormath library.

Now, import the json library and load the color data:

The following function converts colors from hex format (#1a2b3c) to a tuple of integers:

And the following cell creates a dictionary and populates it with mappings from color names to RGB vectors for each color in the data:

Testing it out:

Vector math

Before we keep going, we'll need some functions for performing basic vector "arithmetic." These functions will work with vectors in spaces of any number of dimensions.

The first function returns the Euclidean distance between two points:

The subtractv function subtracts one vector from another:

The addv vector adds two vectors together:

And the meanv function takes a list of vectors and finds their mean or average:

Just as a test, the following cell shows that the distance from "red" to "green" is greater than the distance from "red" to "pink":

Finding the closest item

Just as we wanted to find the animal that most closely matched an arbitrary point in cuteness/size space, we'll want to find the closest color name to an arbitrary point in RGB space. The easiest way to find the closest item to an arbitrary vector is simply to find the distance between the target vector and each item in the space, in turn, then sort the list from closest to farthest. The closest() function below does just that. By default, it returns a list of the ten closest items to the given vector.

Note: Calculating "closest neighbors" like this is fine for the examples in this notebook, but unmanageably slow for vector spaces of any appreciable size. As your vector space grows, you'll want to move to a faster solution, like SciPy's kdtree or Annoy.

Testing it out, we can find the ten colors closest to "red":

... or the ten colors closest to (150, 60, 150):

Color magic

The magical part of representing words as vectors is that the vector operations we defined earlier appear to operate on language the same way they operate on numbers. For example, if we find the word closest to the vector resulting from subtracting "red" from "purple," we get a series of "blue" colors:

This matches our intuition about RGB colors, which is that purple is a combination of red and blue. Take away the red, and blue is all you have left.

You can do something similar with addition. What's blue plus green?

That's right, it's something like turquoise or cyan! What if we find the average of black and white? Predictably, we get gray:

Just as with the tarantula/hamster example from the previous section, we can use color vectors to reason about relationships between colors. In the cell below, finding the difference between "pink" and "red" then adding it to "blue" seems to give us a list of colors that are to blue what pink is to red (i.e., a slightly lighter, less saturated shade):

Another example of color analogies: Navy is to blue as true green/dark grass green is to green:

The examples above are fairly simple from a mathematical perspective but nevertheless feel magical: they're demonstrating that it's possible to use math to reason about how people use language.

Interlude: A Love Poem That Loses Its Way

Doing bad digital humanities with color vectors

With the tools above in hand, we can start using our vectorized knowledge of language toward academic ends. In the following example, I'm going to calculate the average color of Bram Stoker's Dracula.

(Before you proceed, make sure to download the text file from Project Gutenberg and place it in the same directory as this notebook.)

First, we'll load spaCy:

To calculate the average color, we'll follow these steps:

1. Parse the text into words
2. Check every word to see if it names a color in our vector space. If it does, add it to a list of vectors.
3. Find the average of that list of vectors.
4. Find the color(s) closest to that average vector.

The following cell performs steps 1-3:

Now, we'll pass the averaged color vector to the closest() function, yielding... well, it's just a brown mush, which is kinda what you'd expect from adding a bunch of colors together willy-nilly.

On the other hand, here's what we get when we average the colors of Charlotte Perkins Gilman's classic The Yellow Wallpaper. (Download from here and save in the same directory as this notebook if you want to follow along.) The result definitely reflects the content of the story, so maybe we're on to something here.

Exercise for the reader: Use the vector arithmetic functions to rewrite a text, making it...

• more blue (i.e., add colors['blue'] to each occurrence of a color word); or
• more light (i.e., add colors['white'] to each occurrence of a color word); or
• darker (i.e., attenuate each color. You might need to write a vector multiplication function to do this one right.)

Distributional semantics

In the previous section, the examples are interesting because of a simple fact: colors that we think of as similar are "closer" to each other in RGB vector space. In our color vector space, or in our animal cuteness/size space, you can think of the words identified by vectors close to each other as being synonyms, in a sense: they sort of "mean" the same thing. They're also, for many purposes, functionally identical. Think of this in terms of writing, say, a search engine. If someone searches for "mauve trousers," then it's probably also okay to show them results for, say,

That's all well and good for color words, which intuitively seem to exist in a multidimensional continuum of perception, and for our animal space, where we've written out the vectors ahead of time. But what about... arbitrary words? Is it possible to create a vector space for all English words that has this same "closer in space is closer in meaning" property?

To answer that, we have to back up a bit and ask the question: what does meaning mean? No one really knows, but one theory popular among computational linguists, computer scientists and other people who make search engines is the Distributional Hypothesis, which states that:

Linguistic items with similar distributions have similar meanings.

What's meant by "similar distributions" is similar contexts. Take for example the following sentences:

It was really cold yesterday.
It will be really warm today, though.
It'll be really hot tomorrow!
Will it be really cool Tuesday?

According to the Distributional Hypothesis, the words cold, warm, hot and cool must be related in some way (i.e., be close in meaning) because they occur in a similar context, i.e., between the word "really" and a word indicating a particular day. (Likewise, the words yesterday, today, tomorrow and Tuesday must be related, since they occur in the context of a word indicating a temperature.)

In other words, according to the Distributional Hypothesis, a word's meaning is just a big list of all the contexts it occurs in. Two words are closer in meaning if they share contexts.

Word vectors by counting contexts

So how do we turn this insight from the Distributional Hypothesis into a system for creating general-purpose vectors that capture the meaning of words? Maybe you can see where I'm going with this. What if we made a really big spreadsheet that had one column for every context for every word in a given source text. Let's use a small source text to begin with, such as this excerpt from Dickens:

It was the best of times, it was the worst of times.

Such a spreadsheet might look something like this:

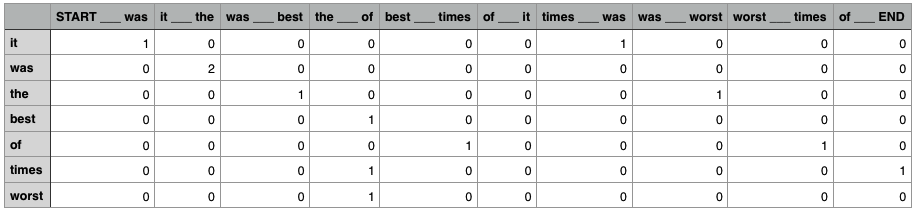
The spreadsheet has one column for every possible context, and one row for every word. The values in each cell correspond with how many times the word occurs in the given context. The numbers in the columns constitute that word's vector, i.e., the vector for the word of is

[0, 0, 0, 0, 1, 0, 0, 0, 1, 0]

Because there are ten possible contexts, this is a ten dimensional space! It might be strange to think of it, but you can do vector arithmetic on vectors with ten dimensions just as easily as you can on vectors with two or three dimensions, and you could use the same distance formula that we defined earlier to get useful information about which vectors in this space are similar to each other. In particular, the vectors for best and worst are actually the same (a distance of zero), since they occur only in the same context (the ___ of):

[0, 0, 0, 1, 0, 0, 0, 0, 0, 0]

Of course, the conventional way of thinking about "best" and "worst" is that they're antonyms, not synonyms. But they're also clearly two words of the same kind, with related meanings (through opposition), a fact that is captured by this distributional model.

Contexts and dimensionality

Of course, in a corpus of any reasonable size, there will be many thousands if not many millions of possible contexts. It's difficult enough working with a vector space of ten dimensions, let alone a vector space of a million dimensions! It turns out, though, that many of the dimensions end up being superfluous and can either be eliminated or combined with other dimensions without significantly affecting the predictive power of the resulting vectors. The process of getting rid of superfluous dimensions in a vector space is called dimensionality reduction, and most implementations of count-based word vectors make use of dimensionality reduction so that the resulting vector space has a reasonable number of dimensions (say, 100—300, depending on the corpus and application).

The question of how to identify a "context" is itself very difficult to answer. In the toy example above, we've said that a "context" is just the word that precedes and the word that follows. Depending on your implementation of this procedure, though, you might want a context with a bigger "window" (e.g., two words before and after), or a non-contiguous window (skip a word before and after the given word). You might exclude certain "function" words like "the" and "of" when determining a word's context, or you might lemmatize the words before you begin your analysis, so two occurrences with different "forms" of the same word count as the same context. These are all questions open to research and debate, and different implementations of procedures for creating count-based word vectors make different decisions on this issue.

GloVe vectors

But you don't have to create your own word vectors from scratch! Many researchers have made downloadable databases of pre-trained vectors. One such project is Stanford's Global Vectors for Word Representation (GloVe). These 300-dimensional vectors are included with spaCy, and they're the vectors we'll be using for the rest of this tutorial.

Word vectors in spaCy

Okay, let's have some fun with real word vectors. We're going to use the GloVe vectors that come with spaCy to creatively analyze and manipulate the text of Bram Stoker's Dracula. First, make sure you've got spacy imported:

The following cell loads the language model and parses the input text:

And the cell below creates a list of unique words (or tokens) in the text, as a list of strings.

You can see the vector of any word in spaCy's vocabulary using the vocab attribute, like so:

For the sake of convenience, the following function gets the vector of a given string from spaCy's vocabulary:

Cosine similarity and finding closest neighbors

The cell below defines a function cosine(), which returns the cosine similarity of two vectors. Cosine similarity is another way of determining how similar two vectors are, which is more suited to high-dimensional spaces. See the Encyclopedia of Distances for more information and even more ways of determining vector similarity.

(You'll need to install numpy to get this to work. If you haven't already: pip install numpy. Use sudo if you need to and make sure you've upgraded to the most recent version of pip with sudo pip install --upgrade pip.)

The following cell shows that the cosine similarity between dog and puppy is larger than the similarity between trousers and octopus, thereby demonstrating that the vectors are working how we expect them to:

The following cell defines a function that iterates through a list of tokens and returns the token whose vector is most similar to a given vector.

Using this function, we can get a list of synonyms, or words closest in meaning (or distribution, depending on how you look at it), to any arbitrary word in spaCy's vocabulary. In the following example, we're finding the words in Dracula closest to "basketball":

Fun with spaCy, Dracula, and vector arithmetic

Now we can start doing vector arithmetic and finding the closest words to the resulting vectors. For example, what word is closest to the halfway point between day and night?

Variations of night and day are still closest, but after that we get words like evening and morning, which are indeed halfway between day and night!

Here are the closest words in Dracula to "wine":

If you subtract "alcohol" from "wine" and find the closest words to the resulting vector, you're left with simply a lovely dinner:

The closest words to "water":

But if you add "frozen" to "water," you get "ice":

You can even do analogies! For example, the words most similar to "grass":

If you take the difference of "blue" and "sky" and add it to grass, you get the analogous word ("green"):

Sentence similarity

To get the vector for a sentence, we simply average its component vectors, like so:

Let's find the sentence in our text file that is closest in "meaning" to an arbitrary input sentence. First, we'll get the list of sentences:

The following function takes a list of sentences from a spaCy parse and compares them to an input sentence, sorting them by cosine similarity.

Here are the sentences in Dracula closest in meaning to "My favorite food is strawberry ice cream." (Extra linebreaks are present because we didn't strip them out when we originally read in the source text.)

Further resources

• Word2vec is another procedure for producing word vectors which uses a predictive approach rather than a context-counting approach. This paper compares and contrasts the two approaches. (Spoiler: it's kind of a wash.)
• If you want to train your own word vectors on a particular corpus, the popular Python library gensim has an implementation of Word2Vec that is relatively easy to use. There's a good tutorial here.
• When you're working with vector spaces with high dimensionality and millions of vectors, iterating through your entire space calculating cosine similarities can be a drag. I use Annoy to make these calculations faster, and you should consider using it too.